1. El teorema de Godel:
Cada hombre está eternamente obligado, en el curso de su breve vida, a elegir entre la esperanza infatigable y la prudente falta de esperanza, entre las delicias del caos y las de la estabilidad.
Marguerite Yourcenar, Memorias de Adriano
Desde muy antiguo se consideró a la matemática, y con bastante justicia, como la reina de las ciencias. Este precepto, cuando Galileo en el siglo XVII proclamó que "el libro de la naturaleza está escrito con caracteres matemáticos", confirió a la corona los atributos del derecho divino. Y hasta cierto punto, los de una monarquía absoluta. Si bien las matemáticas nunca parafrasearon a Luis XIV diciendo: "la ciencia soy yo", fue tan sólo porque son incapaces de hablar (y tal vez por falsa modestia). Lo cierto es que, a partir del triunfo de la mecánica newtoniana, las matemáticas se convirtieron en la aspiración común de todas las disciplinas científicas: matematizar una ciencia garantizaba su verdad. Es preciso reconocer, de paso, y a despecho de cualquier aspiración republicana, que este sistema de gobierno dio resultados espectaculares: la reducción de las ciencias a fórmulas y el manipuleo de ellas produjeron la acumulación de conocimientos más formidable que recuerde la memoria humana.
Ese papel central de la matemática deviene de su método: la obtención de resultados mediante la deducción puramente lógica a partir de un puñado de axiomas elementales que se aceptan como verdaderos: de hecho, ésta fue la metodología que utilizó Euclides en sus célebres Elementos de Geometría, que usaron sin mayores variantes hasta hace ciento cincuenta años, y permanecen, sin demasiadas transformaciones en los textos de geometría que se utilizan aún hoy en la escuela secundaria.
Es verdad que durante el siglo pasado, la supuesta verdad absoluta de los axiomas de la geometría euclideana recibió un duro golpe: partiendo de axiomas diferentes a los de Euclides, Lobachevsky y Riemann construyeron geometrías perfectamente coherentes, aunque distintas de la euclídea, y de alguna manera, la búsqueda de la verdad fue sustituida por el afán de coherencia y no contradicción.
Hacia finales de siglo, el triunfo del método axiomoático era completo: las investigaciones de la lógica matemática se dirigían con especial énfasis a buscar una formalización y axiomatización de toda la matemática.
La idea se inscribía perfectamente en la muy finisecular concepción del progreso: una vez encontrados los axiomas adecuados, todas las verdades podrían ser deducidas a partir de ellos, mediante la lógica y la paciencia. Cuando en 1900 el gran matemático David Hilbert presentó un programa enunciando la lista de problemas matemáticos pendientes (apenas un puñado), hizo un alarde de confianza: resolverlos era sólo cuestión de tiempo. La potencia de las matemáticas parecía infinita, y siguió pareciendo infinita hasta 1931.
Porque en ese año, en efecto, el matemático y lógico Kurt Gödel demostró un teorema que se transformó en un clásico de la lógica matemática y que, por su importancia (y su exquisita belleza), se conoce como "el teorema de Gödel, 1931", (y también como el teorema que asegura la incompletitud de la aritmética). En él se demuestra que no todas las verdades matemáticas pueden ser alcanzadas. Más sencillamente: que en cualquier sistema que contenga la aritmética, existe por lo menos una fórmula, que, aun siendo verdadera, no podrá jamás ser demostrada. No importa cuál sea el conjunto de axiomas que se use: siempre habrá algo, que, si bien es verdadero, no se puede demostrar.
Es decir: en el seno mismo de las matemáticas, hay cosas no alcanzables, lugares a donde la paciente deducción no llegará jamás.
Naturalmente, este curioso resultado, no afecta para nada a la utilización de la matemática por el resto de los científicos, ni al papel central que ésta juega en todo el sistema de las ciencias. Pero de alguna manera, limita su omnipotencia. Desde la
Revolución Francesa en adelante, y como bien lo pudo comprobar Luis XVI, ya se sabe que las monarquías absolutas no son del todo seguras, y si bien no es cierto que las matemáticas hayan perdido su cetro, puede decirse que su largo y glorioso reinado, desde el teorema de Gödel en adelante, adquirió los contornos de una monarquía constitucional.
2. La paradoja de Wittgenstein
«Nuestra paradoja era ésta: una regla no podía determinar ningún curso de acción porque todo curso de acción puede hacerse concordar con la regla. La respuesta era: Si todo puede hacerse concordar con la regla, entonces también puede hacerse discordar. De donde no habría ni concordancia ni desacuerdo.»
La obra de L. Wittgenstein es un eslabón fundamental en el proceso de racionalización y desencanto que, entre otras cosas, caracteriza nuestro mundo. En una de sus primeras reflexiones se preguntaba: « ¿Qué sé sobre Dios y la finalidad de la vida?», e inmediatamente respondía: «Sé que este mundo existe. Que estoy situado en él como mi ojo en su campo visual. Que hay en él algo problemático que llamamos su sentido... Que podemos llamar Dios al sentido de la vida, esto es, al sentido del mundo. » Esta reflexión sobre el sentido del mundo y de la vida, tan fundamental en el ser humano y en la Filosofía, en concreto, hará que para el vienés cobre especial importancia el estudio de cómo se sitúa y se relaciona el ojo (la palabra, la idea) con respecto a su campo visual (campo de significado, de entendimiento), esto es, la indagación sobre los medios y bases posibilitantes de la captación del sentido. Esta cuestión está, en última instancia y genéticamente, tras el problema de la representación.
Una indagación de ese calibre puede llevar a caminar sobre los limites del sentido, incluso a caer en el turbio sinsentido. El peligro se hace inevitable para quien afronta esa reflexión con la radicalidad y la implicación personal con que Wittgenstein lo hizo. «Al filosofar hay que bajar al viejo caos y sentirse a gusto en él», dirá ya en plena madurez. No puede extrañarnos, por tanto, que en la caracterización de ese dramatis personae que Ludwig fue construyendo aparezca, en lo vital y en lo filosófico metodológico, el rasgo de paradójico. Wittgenstein es una pregunta a la que no es posible dar respuesta, ha escrito 1. Bernhard. De todos es conocido cómo el Tractatus concluye declarando carentes de sentido a sus proposiciones más esclarecedoras: peldaños de una escalera que una vez subida es arrojada.
La complejidad, profundidad y originalidad del pensamiento wittgensteiniano hacen difícil y duro su seguimiento. Por otro lado, la fuerte personalidad y la capacidad persuasiva que en él también hay hacen que, una vez introducidos en su obra, ésta nos desborde por todos lados y, como «epígonos insignificantes», se tienda a convertir un pensamiento vivo en una jerga. Quizá ello ha favorecido el cumplimiento de la amenaza que sobre el trabajo de Wittgenstein predecía quien le conoció íntimamente durante los últimos treinta años de su vida: «Sería una tragedia que estudiosos bienintencionados pretendieran hacer aparecer que sus escritos fueran ahora fácilmente asimilables, precisamente en un medio intelectual contra el que aquéllos suponían una prevención profunda. Espero no colaborar ni en esa tendencia, que ha venido devorando el legado de Wittgenstein, ni en la mistificación de un pensador. Mis únicos propósitos en este escrito son: 1) situar e identificar una cuestión que parece primordial en su obra, especialmente en las Investigaciones Filosóficas. 2) presentar esa cuestión como un grave problema para la perspectiva dominante; 3) fundamentar el reconocimiento del problema, de las falsas soluciones que se le han venido dando y de los supuestos que lo alimentan; y 4) aclarar las consecuencias del problema, apuntando, a la vez, el camino que parece sacarnos de él. Entiendo que la mejor reflexión sobre el pensamiento de Wittgenstein es la que se hace a partir de él.
3. Que es una sucesión. La sucesión de Fibonacci:
En terminología matemática se incluye sucesión para designar la existencia de elementos encadenados o sucesivos.
Se excluye totalmente la sinonimia con el término serie.
En textos académicos se suele llamar simplemente sucesión con el bien entendido que todas son del mismo tipo. Esto no impide la existencia de sucesiones de diversas entidades matemáticas.
Cuando abundan sucesiones de todo tipo se puede cambiar incluso el nombre de sucesión por otro.
La sucesión de Fibonacci es la sucesión de números:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
Cada número se calcula sumando los dos anteriores a él.
· El 2 se calcula sumando (1+1)
· Análogamente, el 3 es sólo (1+2),
· Y el 5 es (2+3),
· ¡y sigue!
Ejemplo: el siguiente número en la sucesión de arriba sería (21+34) = 55
¡Así de simple!
Aquí hay una lista más larga:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...
La regla
La sucesión de Fibonacci se puede escribir como una "regla" (lee sucesiones y series):
la regla es xn = xn-1 + xn-2 donde:
· xn es el término en posición "n"
· xn-1 es el término anterior (n-1)
· xn-2 es el anterior a ese (n-2)
Por ejemplo el sexto término se calcularía así:
x6 = x6-1 + x6-2 = x5 + x4 = 5 + 3 = 8
Razón de oro
Y hay una sorpresa. Si tomas dos números de Fibonacci consecutivos (uno detrás del otro), su cociente está muy cerca de la razón áurea "φ" que tiene el valor aproximado 1.618034...
Usar la razón de oro para calcular números de Fibonacci
Y es más sorprendente todavía esta fórmula para calcular cualquier número de Fibonacci usando la razón de oro:
Increíblemente el valor siempre es un número entero, exactamente igual a la suma de los dos términos anteriores.
Ejemplo:
Cuando usé una calculadora para hacerlo (con sólo 6 decimales para la razón aúrea) obtuve la respuesta 8.00000033. Un cálculo más exacto habría dado un valor más cercano a 8.

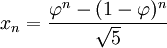
No hay comentarios:
Publicar un comentario